梁薇成都嘉祥外国语学校成华校区

摘要：数学几何概念是发展学生逻辑论证、合情推理和空间想象力的前提。而现今的教学中，部分几何概念课教学的模式较为单一，教师在教学过程中忽视了学生对几何概念知识网络的建构。针对此问题，本文设计了调查问卷，通过教学实践中的具体案例，引入思维导图这一可视化思维工具。从引入概念、理解概念、深化概念和构建知识网络四个方面，对数学几何概念的教学方法进行总结提炼，获得了有效几何概念教学的经验。本文研究结果对培养学生数学思维能力，实现学生对数学知识的自我组织具有重要的促进作用。

关键字：思维导图;初中数学;几何概念;课堂教学;有效性

Abstract:The concept of mathematical geometry is the prerequisite for the development of students' logical argumentation, sensible reasoning and spatial imagination. In today's teaching, the teaching mode of some geometric concept classes is relatively simple, and the teachers neglect the students' construction of the geometric concept knowledge network in the teaching process. In response to this problem, this paper designed a questionnaire to introduce a visual thinking tool through mind mapping through specific cases in teaching practice. From the four aspects of introducing concepts, understanding concepts, deepening concepts and constructing knowledge networks, the teaching methods of mathematical geometric concepts were summarized and refined, and the experience of effective geometric concept teaching is obtained. The research results of this paper have an important role in cultivating students' mathematical thinking ability and realizing students' self-organization of mathematics knowledge.

Keywords:mind map;junior high school mathematics;geometric concept;classroom teaching;effectiveness

一、引言

数学概念是数学学习定理、法则、公式的基础，也是数学思想方法的出发点和解决数学问题的前提。数学几何概念更是发展逻辑论证、合情推理和空间想象力的前提。而现今的教学中，部分几何概念课教学的模式显得较为单一，教师在教学过程中重教而忽视了学生对几何概念形成过程和知识的建构，重概念讲授而忽视了学生的思维能力的培养。思维能力作为核心素养的核心能力，在新一轮的教育改革中备受关注。而八大思维图示法、思维导图、概念图^[1]成为有效促进数学思维能力的手段。现实中，教师虽然尝试运用思维可视化工具参与教学，但关于思维导图如何在几何概念教学中有效使用的相关研究很少。

针对以上问题，本文通过设计调查问卷了解现实几何概念教学中存在的现状及问题，通过教学实践中的案例，引入思维导图这一可视化思维工具，从引入概念，理解概念，深化概念，构建知识网络四个方面对数学几何概念的教学方法进行总结提炼，从而获得几何概念有效教学的经验。以培养学生数学思维能力，真正达到学生对数学知识的自我组织。

二、初中数学几何概念

数学概念是反映事物在数量关系和空间形式属性的抽象思维形式^[2]，是数学最基础的表达形式。在小学阶段，由于小学生思维的形象性，对于数学概念大都用一些描述性的语言来表述。而在初中阶段对概念的描述更加准确，同时概念所覆盖的内容要远远多于定义所表达的内容^[3]。数学概念作为数学思想方法的出发点和解决数学问题的前提，有助于学生对定理、定义、公式、法则的理解，帮助形成数学的基础知识体系，训练数学基本技能，领悟数学中基本思想，积累基本数学活动经验。同时也是培养学生数学抽象能力，逻辑推理能力，数学建模能力，直观想象能力等核心素养的体现。其中，几何概念作为数学概念的重要组成部分，除了具备数学概念相同的形式和结构外，还具有如下的特殊思维形式特征^[4]：

1.几何概念往往来自现实世界中的直观模型。如三角形、圆等。

2.几何概念具备高度概括的特点。

3.几何概念与相应的几何表述语言、图形和符号表达紧密相连，有独特的符号语言体系。

4.图形本身就具备概念性。如三角形的图形就包含着三角形的概念“由不在同一直线上的三条线段首尾顺次连接而形成的平面图形”及三角形三边关系等信息。

新课程标准的初中数学课程内容包括四大板块：数与代数、图形与几何、统计与概率、综合与实践^[5]。其中图形与几何部分对发展学生的空间观念和几何直观，培养学生的合情推理能力，积累几何活动经验起着重要的作用。同时，图形与几何在成都市中考试题中占35%—40%，也有着重要的地位。对现阶段的几何概念教学现状调查也有着实际的意义。

三、数学几何概念教学现状分析

（一）教师教学形式单一，重结果轻过程。现阶段，数学教学仍然受到应试教育较大的影响。教学中，教师重教授而轻视学生知识习得的过程，重题目训练而忽视思维的培养。教学的急功近利使几何概念课的教学中常出现用课堂上20%的时间给出概念，80%的时间用于习题的训练。忽视了学生几何概念形成这一思维过程，学生并没有深入理解概念。

（二）学生对几何概念课的不重视及对几何概念教学的需求。在与学生的访谈中发现，部分学生对于几何概念课的感受是总以冗长的文字出现，觉得只要会解题，概念是否掌握影响不大。学生在练习和测验中也较少将错因归于数学概念的不清，常以粗心、马虎盖过问题的本质。由此可见，学生对于数学几何概念课并未引起足够的重视。另一方面，为了更好地了解学生对几何概念课学习的情况，对我校8年级学生中随机选取了105名学生进行了有关数学概念教学的问卷调查，调查问卷中的部分典型问题如表1所示。

表1. 关于数学概念的问卷调查表

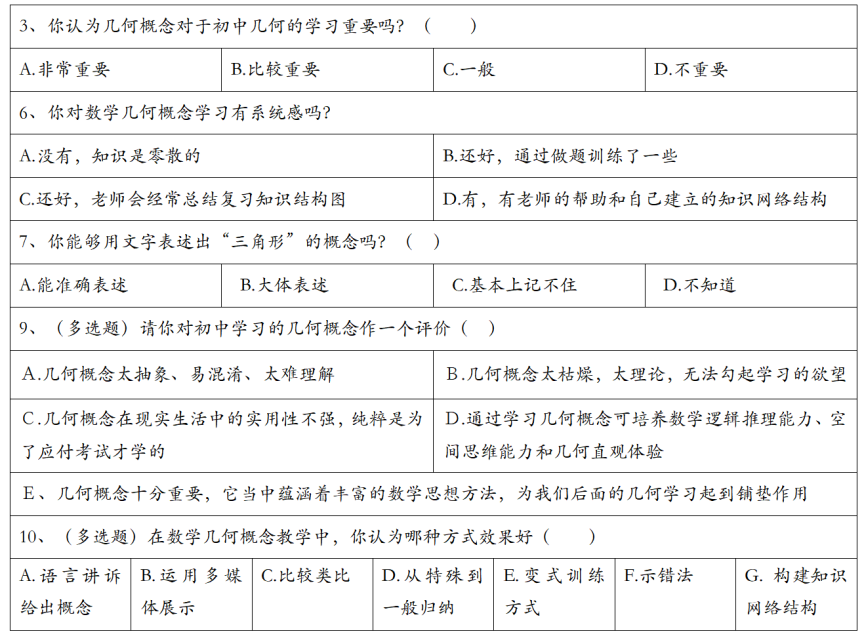
通过问卷的调查结果分析，图1反映出有40%的学生认为几何概念一般重要，通过访谈，部分学生认为在几何解题中对于概念的直接运用较少，几何证明的思路更为重要。学生对几何概念重视程度上的差异，在一定程度上降低了课堂教学的有效性。图3的结果也进一步验证了此问题，大部分同学并不能够用准确的语言对于已学概念“三角形”进行描述，究其原因，还是对于几何概念的理解上不够深入。

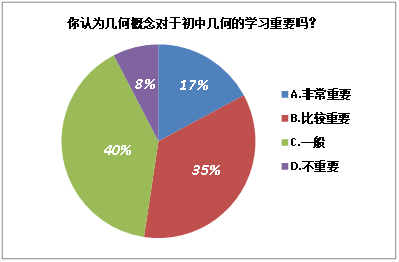
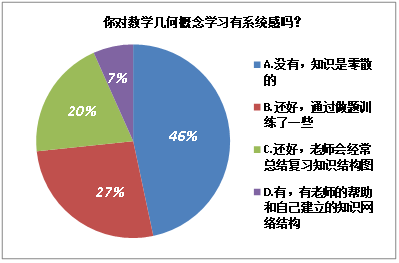
图1. 几何概念重要性调查结果 图2. 几何概念学习系统感调查结果

由图2结果，反映出大多数学生并没有建立几何概念知识体系的意识，仅有7%的同学表示自己有建立知识网络。也正由于知识结构的缺失，学生对几何概念的内涵与外延都无法准确掌握。图4结果显示，学生中有63人表示几何概念太抽象、易混淆、难以理解。而图5结果显示，学生更希望能够在几何概念的教学中构建起几何概念的知识网络结构、通过类比、

图3. “三角形”概念表述调查结果

从特殊到一般的归纳方式来探索和生成概念。调查的结果可以看出，直接给出概念的教学模式已经不适应现今的课堂，学生对于数学概念课有更多的期待和要求。在培养学生数学核心素养的大背景下，对概念课教学的有效性分析就显得尤为重要了。

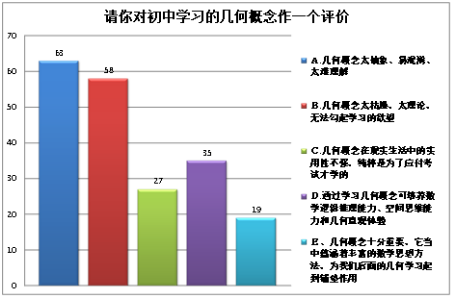
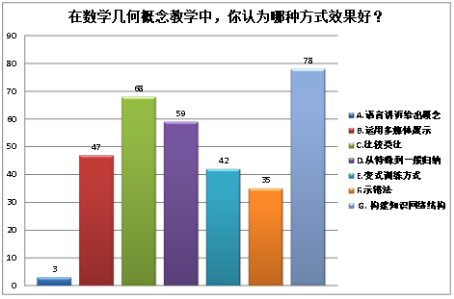
图4. 评价几何概念学习调查结果图5. 几何概念教学方式效果调查结果

四、几何概念课教学的有效性分析

课堂教学实质是教师在教学目标的指导下有计划地实现学生有效学习的过程^[6]。有效课堂的关键是学生的进步与发展。应关注在教学过程中，是否完成了教学目标，使得知识与技能，过程与方法，情感态度与价值观，思维目标得以实现。是否使学生参与到了教学过程中，是否培养了学生的思维，使学生有进一步学习的兴趣。通过以上分析，作为一堂有效的几何概念课应该具有以下特征：

1.设计明确清晰的教学目标；

2.基于学生已有的知识和经验背景设计教学过程；

3.几何概念形成过程中学生的实质性参与其中；

4.学生能准确把握几何概念的外延与内涵；

5.学生能够将几何概念应用于实际问题；

6.能够培养学生的数学思维能力，形成核心素养。

基于以上的特征，思维导图的引入在数学几何概念的教学中就有着实际意义。

五、思维导图应用于初中几何概念教学的意义

20世纪60年代英国心理学家东尼·博赞提出了思维导图的概念^[7]。而如今八大思维图示、思维导图和概念图已成为中小学应用广泛的思维可视化工具，如图表2。初中是数学学习的重要阶段，几何学习中所涉及到的知识点繁多，灵活性大、综合性很强。如何让学生夯实基础知识，深入理解概念，将学到的零散的、细碎的概念综合起来，以达到对知识的有机整合，思维导图就是实现这一目标的理想选择。其作用可归结为以下几点：

（一）有助于学生形成知识网络

在数学教材的编排中，初中的几何知识本身有逻辑关系、层次性及整体性。但在课堂教学中存在着一定的局限性，知识的逻辑性、层次性及整体性并没有充分体现出来。而思维导图以可视化、结构化的形式展现知识，以多色彩、层次分明的直观形象将新旧知识联系，将易混淆知识类比^[8]。让学生在学习过程中构建起几何概念之间的内在逻辑关系，将新知识与原有认知结构相联系，有助于学生全面掌握知识。

表2.八大思维图示法、思维导图、概念图的作用及特点^[1]

（二）有助于提高学生的思维能力

思维导图有助于培养学生的发散性思维品质。思维导图的创作过程能增加学生在短时间内能连续地表达出的观念和设想的数量；让学生学会从不同角度、不同方向灵活地思考问题；激发出具有独特解决问题的方法和别出新意的思路；能在头脑中构想并描述事物的具体细节。利用思维导图，学生能够更系统地存储、管理、应用知识，有条理地掌握各几何概念之间的关系，促进学生逻辑思维品质的发展。

（三）有利于学生创新思维的培养

在几何概念的教学中，教师可通过问题的引导充分给予学生自主探索的空间，创造出符合自己思维逻辑的知识结构图。在此过程中，学生的想象力、自主探索能力、合作分享的能力都得到了锻炼。学生学会突破原有的思维定势，更开放性的思考问题，多角度的解决问题。因此，研究如何利用思维导图构建有效的数学几何概念课教学，对培养学生思维能力，提升教学质量有重要作用。

六、思维导图在初中数学几何概念教学中的有效性研究

（一）联想回顾、引入概念

概念课的引入是课堂教学的开端，也是形成概念的基础。有效的概念引入，能够迅速调动学生学习的积极性，进入到教学情境，帮助学生更好地接受和理解概念。

1.梳理知识，复习回顾

通过树形图或括号图对之前已学知识进行梳理。如学习《平行四边形》这一课，学生在

小学已经认识过平行四边形，并对几类特殊的四边形都有一定的了解。因此，教师可以在学生已有的认知结构上设计引入。提出问题“在小学我们都认识过哪些四边形？”，将学生回答的零散答案根据一定的分类标准进行分类。如图6，将四边形根据是否有一组对边平行分为一般四边形和特殊四边形。再将特殊四边分为平行四边形和梯形，而平行四边形下又包含长方形、正方形、菱形。通过图文并茂的形式，完善学生之前的知识结构，也为后面学习特殊平行四边形起到铺垫的作用。

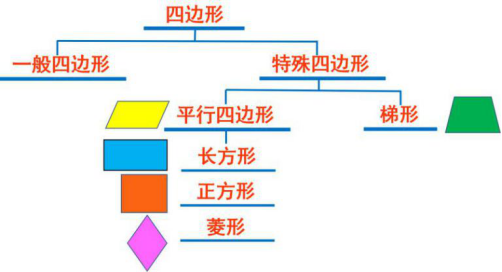
图6. 四边形分类树形图

2.充分联想，激活思维

运用圆圈图，让学生对所学内容展开充分联想。如在学习《平行四边形》这一课中，为引入平行四边形的概念，让学生对平行四边形展开充分的联想，尽可能多地写出与平行四边形相关的关键词。如图7，看似杂乱的词语，却能从中梳理出平行四边形的定义（两组对边分别平行）、基本元素（边、角、对角线）及性质（内角和为360°，没有稳定性等），同时还将平行四边形与我们的生活紧密联系起来（笔记本、门窗等）。充分调动了学生的积极性，更是展现出了许多课本中没有涉及到却与之相关的内容，发展了学生的发散能力和创新能力。同时也展现了几何概念的直观性。当然，在此过程中，教师一定要引导学生对联想到得关键词进行逆向筛选，归类总结。

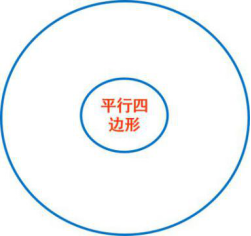
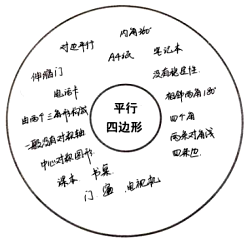
(a) (b)

图7. 平行四边形联想圆圈图

（二）深入剖析、理解概念

学生是否能够清晰地理解概念，并运用概念解决实际问题，对概念的深入剖析和理解是非常重要的一个环节。理解概念的过程，也是培养学生辩证地思考问题的过程，更有助于培养思维的深刻性。概念的理解应该抓住概念的实质性特征，联系符号、文字、图形、关键条件等方面综合的理解分析归纳。而思维导图也正是将符号、文字、图形融为一个整体的可视化工具，以帮助学生深层次的理解和掌握概念。如图8，在《黄金分割》中讲解概念后，剖析概念中线段之间的比例关系、比例中项关系、黄金比的具体值，而这三个关系均是由C是线段AB的黄金分割点得出，渗透转化的思想，深入剖析了概念，抓注了概念的本质。

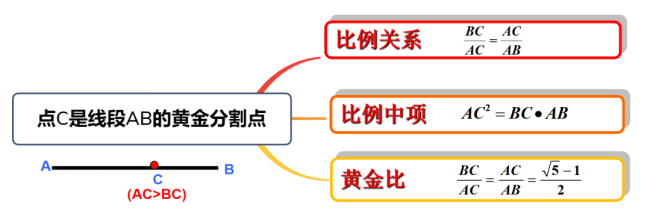
图8. 黄金分割概念剖析思维导图

（三）类比理解、深化概念

通过对北师大版初中数学教材的分析发现，属加种差形式定义^[9]是初中数学几何概念的主要定义方式。用公式表示为：被定义项=种差+邻近的属。例如矩形的定义：有一个角是直角的平行四边形叫矩形。用公式表示为：矩形=有一个角是直角（种差）+平行四边形（属）。这样的定义方式体现了几何概念的层次性，体系性。需要学生在新旧数学概念之间建立起联系，明确概念的内涵与外延，将已有认知结构中的数学概念与新概念进行区分，类比，整合成一个新的知识体系，达到概念的同化。而双气泡图这种思维图示工具可以有效地帮助学生将新旧概念进行对比，比较发现异同，从而发现和总结出概念所反映的规律与本质属性。同时结合“数学思想”为催化剂，实现概念间的类比迁移^[10]。

如中心对称与中心对称图形的概念，在教材中是一节课呈现的内容，不少学生都感觉概念中的文字信息量大且相似点多，不易准确把握概念。如图9，我们将两个概念进行类比分析，概念间的联系与区别就显得清楚明确了。

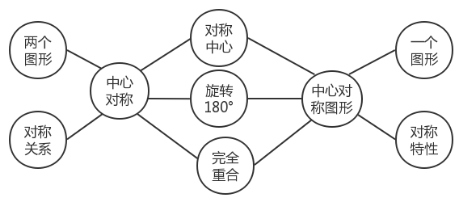
图9. 中心对称与中心对称图形双气泡图

同样，在特殊平行四边形这一章中，矩形、菱形、正方形等特殊四边形的性质定理及判定定理较多，且彼此之间存在区别和联系，极易混淆，如果运用线性的笔记方式，学生不易记忆、理解和区分。下面以矩形和菱形的性质为例设计双气泡图，如图10。将矩形与菱形的相同性质放在中间，从边、角、对角线三个方面对应描述不同性质，以达到对比理解的目的。

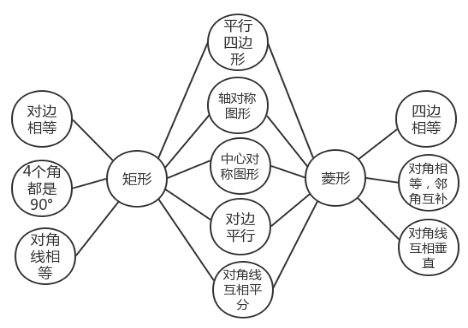
图10. 中心对称与中心对称图形双气泡图

（四）建构知识网络、提升整体思维

《数学课程标准解读》指出：“数学教育的价值并非单纯地通过积累数学事实来实现，它更多地通过对重要的数学思想方法的领悟，对数学活动经验的条理化，对数学知识的自我组织等活动来实现。”^[11]数学知识的自我组织，就是学生能够主动将已学过的零散知识，根据自己的理解和认识，进行重新提炼，组织，构建知识网络。学生在这个“再创造”的过程中，能主动探索思考数学概念性知识之间的内在联系，形成整体性和个性化的认识。而思维导图能够直观形象的呈现知识间的关联，提高学生对数学概念性知识的分析重组能力，帮助学习者组织起适当的知识网络结构，体现思维过程，提升思维能力。

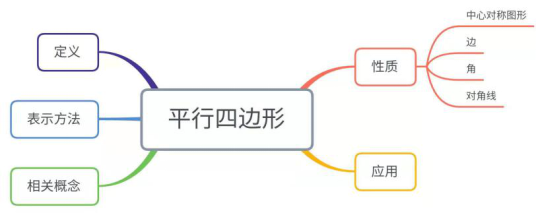
图11. 《平行四边形》思维导图

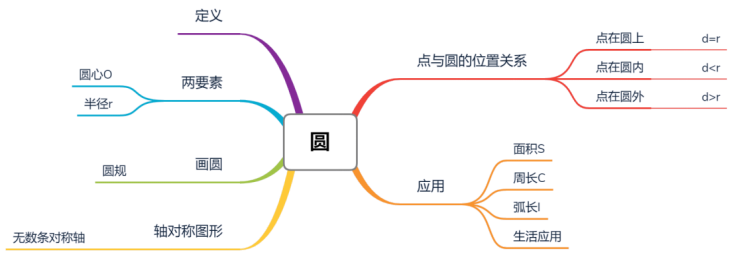
图12. 《圆》思维导图

如图11、图12均是作为概念课的第一课时的教学内容以思维导图的形式所呈现的知识结构，以《平行四边形》为例，在教学内容中除了平行四边形的定义外，还包括表示方法、相关概念、性质及应用的相关知识。通过思维导图的呈现，本节课的教学内容以可视化的思维结构呈现在学生的面前，更有助于学生的理解掌握。当然，建构知识结构的思维导图可以以一节课的内容来呈现，也可以按章节的方式来呈现。思维导图的绘制过程可以以教师板书的形式呈现，但更为有效的是体现学生思维过程自主的绘制，以体现学生思维过程，达到个性化的发展。如图13，是学生绘制的三角形章节知识网络结构图。

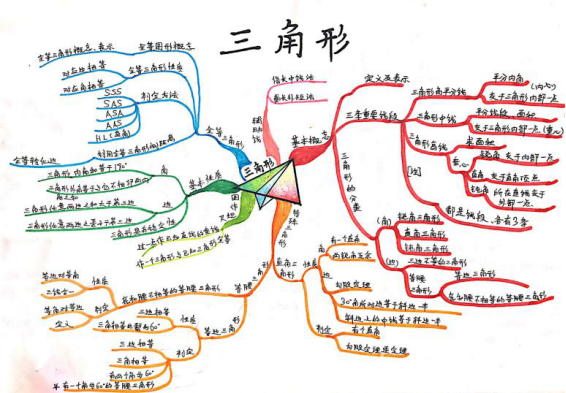
图13. 《三角形》章节思维导图

七、结论

数学几何概念作为数学知识体系中的重要组成部分，是发展逻辑论证、合情推理和空间想象能力的前提^[12]，在数学教学中也占据着基础性的地位。本文通过在教学实践中的案例研究，引入思维导图这一可视化思维工具，从引入概念，理解概念，深化概念，构建知识网络四个方面对数学几何概念的教学方法进行总结提炼，从而获得几何概念有效教学的经验。以培养学生数学思维能力，真正达到学生对数学知识的自我组织。

参考文献：

[1]赵国庆，杨宣洋，熊雅雯.论思维可视化工具教学应用的原则和着力点[J].课程与教学，2019（9）

[2]田万海.数学教育学[M].浙江：浙江教育出版社，1993：166

[3]朱水根，王延文.中学数学教学导论[M].北京：教育科学出版社，2001:261

[4]白姝园.初中数学核心知识与思维导图的设计与实践研究[D].北京：北京师范大学，2017：43

[5]中华人民共和国教育部.全日制义务教育数学课程标准[M].北京:人民教育出版社，2011

[6]余文森.大夏书系·有效教学：有效教学十讲[M].上海：华东师范大学出版社，2009

[7]东尼·博赞.思维导图[M].北京：中信出版社，2009：4-7

[8]商庆平.基于思维导图支架的数学概念可视化研究[J].教学与管理，2013（1）

[9]曹一鸣.数学教学论[M].北京：高等教育出版社，2008:207

[10]李红婷.7-9年级学生几何推理能力发展及其教学研究[D].重庆：西南大学，2007

[11]教育部.基础教育课程教材专家工作委会编数学课程标准（年版）解读[M].北京：北京师范大

学出版社，2012：246

[12]江小燕.新课程下初中几何有效教学的实践与探索[D].福建：福建师范大学，2013

[13]张朝亚.浅谈初中几何概念教学策略[J].数理化学习，2012(12)

[14]王玉荣.核心素养导向下的初中数学课堂有效性探究[J].数理化解题研究，2018（8）

[15]邱燕华.核心素养下的概念教学策略，江西教育[J],2018（3）

[16]王菠.利用思维导图优化初中数学复习课[D].南京：南京师范大学，2014

[17](美)林恩·埃里克森著.概念为本的课程与教学[M].兰英译.北京：中国轻工业出版社，2003

[18]龙宝新.聚焦核心知识的高效课堂教学实验设计[J].当代教师教育，2012（2）

[19]吴志丹.协作建构思维导图在数学复习课中的应用探究[J].电化教育研究，2010（7）

[20]方永进.“思维导图”是数学课本不错的“补钉”[J].浙江教育科学，2011⑷

[21]陈霞.运用思维导图促进初中生数学理解的研究[D].广西：广西师范大学，2012

---

附录：

初中数学几何概念教学调查问卷

亲爱的同学：

您好！这是一项关于初中数学几何概念学习方面的调查问卷。旨在了解初中数学几何概念教学及学习过程中的问题，以指导今后的数学几何概念教学。此问卷不记名，不考虑对错，请根据实际情况如实作答。感谢您的支持，谢谢！

1、你觉得几何概念难吗？ ( )

A.很难 B.难 C.还好 D.不难

2、你认为学习几何与学习代数方法有变化吗？（ ）

A.有变化，觉得原方法不适用，试图改进，但不知从何下手或没效果

B.有变化，改进了许多，学起来得心应手

C.没想过，我认为学得好坏与学习方法无关

D.没变化，照样能应付

3、你认为几何概念对于初中几何的学习重要吗？（ ）

A.非常重要 B.比较重要 C.一般 D.不重要

4、你认为学习几何概念或定理最关注的应是（ ）

A.概念定理的产生形成和发展过程 B.如何记忆概念定理公式

C.如何应用概念定理 D.概念定理的几何意义 E.其他

5、数学考试中，在几何概念相关题目方面的失分情况（ ）

A.很多 B.较多 C.一般 D.很少

6、你对数学几何概念学习有系统感吗？

A.没有，知识是零散的 B.还好，通过做题训练了一些

C.还好，老师会经常总结复习知识结构图 D.有，有老师的帮助和自己建立的知识网络结构

7、你能够用文字表述出“三角形”的概念吗？（ ）

A.能准确表述 B.大体表述 C.基本上记不住 D.不知道

8、在几何概念学习过程中，就你个人而言，你认为有效的学习方式是（ ）

Ａ.记忆解题法 Ｂ.公式法则套用 Ｃ.自主合作探究 Ｄ.讲练结合

9、（多选题）请你对初中学习的几何概念作一个评价（ ）

Ａ.几何概念太抽象、易混淆、太难理解

Ｂ.几何概念太枯燥，太理论，无法勾起学习的欲望

Ｃ.几何概念在现实生活中的实用性不强，纯粹是为了应付考试才学的

Ｄ.通过学习几何概念可培养数学逻辑推理能力、空间思维能力和几何直观体验

Ｅ.几何概念十分重要，它当中蕴涵着丰富的数学思想方法，为我们后面的几何学习起到铺垫作用

10、（多选题）在数学几何概念教学中，你认为哪种方式效果好（）

A.语言讲诉给出概念 B.运用多媒体展示 C.比较类比 D.从特殊到一般归纳

E.变式训练方式 F.示错法 G.构建知识网络结构